Distancia hiperfocal

La distancia hiperfocal es un concepto relacionado con la Profundidad de Campo. Pero es tan importante que he decidido hacer un spin-off sobre la distancia hiperfocal.

Lo primero es entender lo que es, porque hay mucha confusión al respecto.

La profundidad de campo aumenta con la distancia de enfoque. Para hacer más sencilla la explicación, considera tan sólo la profundidad de campo por detrás del plano enfocado.

Por ejemplo, imagina que enfocas a 1 m y que se ve aceptablemente nítido hasta 3 m. En ese caso, la profundidad de campo por detrás es de 3 - 1 = 2 m.

Ahora, sin moverte del sitio, enfocas un poco más atrás, por ejemplo a 5 m. Y compruebas viendo la foto que se ve aceptablemente nítido hasta 20 m. En esta segunda foto, la profundidad de campo por detrás es 20 - 5 = 15 m.

Como ves, la segunda foto tiene más profundidad de campo por detrás (15 m) que la primera (2 m). Es decir, la profundidad de campo por detrás aumenta a medida que aumentas la distancia de enfoque.

Si sigues enfocando cada vez más lejos, llegará una distancia (por ejemplo, 10 m) donde la profundidad de campo por detrás llegará hasta infinito; es decir, verás todo lo que hay por detrás del plano enfocado aceptablemente nítido.

Esa distancia es lo que se llama distancia hiperfocal.

Resumiendo, la hiperfocal es una distancia de enfoque muy particular: aquélla que hace que la profundidad de campo por detrás llegue hasta infinito.

¿Y por delante? Pues cuando enfocas a la hiperfocal, la profundidad de campo por delante es justo la mitad; siguiendo con nuestro ejemplo, si la hiperfocal es 10 m, esto quiere decir que verás aceptablemente nítido desde 5 m (la mitad de la hiperfocal) hasta infinito.

Francamente, conozco conceptos en fotografía más complejos que este, así que no entiendo por qué tanto lío con la hiperfocal.

Parte de la explicación de este lío la tienes en el vídeo: algunos tutoriales sobre la hiperfocal son muy confusos, otros les falta rigor y algunos otros simplemente no saben lo que es la hiperfocal. Así es muy difícil aprender. Por supuesto los hay donde lo explican muy bien; !pero cómo distinguirlos si no sabes lo que es la hiperfocal!

Hay otra definición de hiperfocal: cuando enfocas a infinito (ahora no enfocas a la hiperfocal, sino a infinito), la profundidad de campo va desde la hiperfocal hasta infinito.

Es decir, en esta segunda definición, la profundidad de campo por delante va desde infinito hasta la hiperfocal. Siguiendo con nuestro ejemplo anterior, si enfocases esa foto a infinito (en vez de a 10 m), verías que sale aceptablemente nítido desde 10 m hasta infinito.

Compara los dos casos: en el primero (enfoque a 10 m, la hiperfocal), la profundidad de campo va de 5 m a infinito; en el segundo (enfoque a infinito), la profundidad de campo va de 10 m (la hiperfocal) hasta infinito.

Es decir, cuando enfocamos a infinito perdemos profundidad de campo, en este caso 5 m. Por eso se dice que la distancia hiperfocal es la distancia de enfoque que maximiza la profundidad de campo.

Si enfocas un poco más cerca que la hiperfocal, el fondo ya no te sale aceptablemente nítido, con lo que la profundidad de campo ya no llega hasta infinito por detrás.

Si enfocas un poco más lejos, el fondo sale aceptablemente nítido, pero pierdes profundidad de campo por delante. El caso límite es cuando enfocas a infinito; en ese caso la profundidad de campo por delante empieza en la distancia hiperfocal.

Ahora que ya tienes claro lo que es, puedes ver lo que no es, los errores más típicos que se cometen al hablar de la hiperfocal.

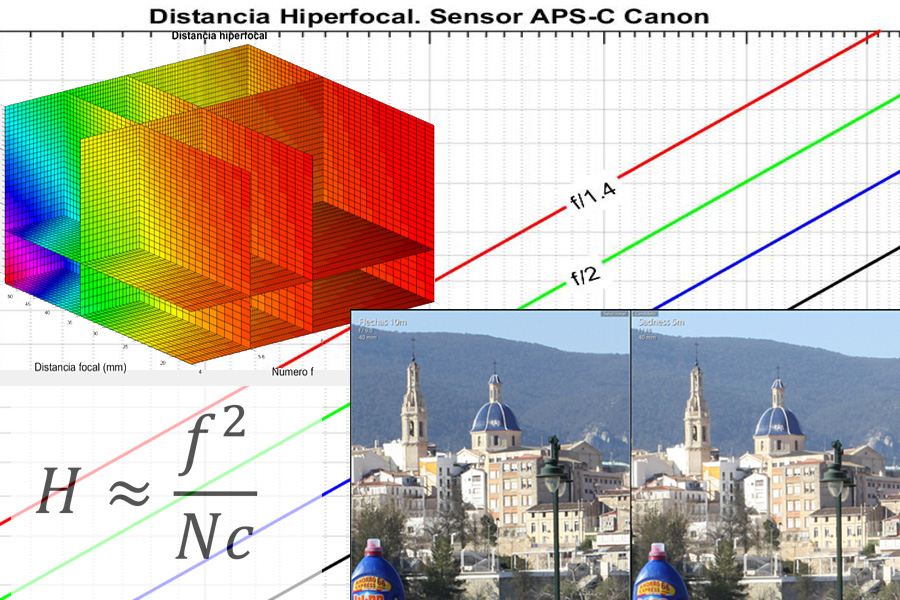
La fórmula de la distancia hiperfocal $$D_h$$ es:

donde f es la distancia focal, c el diámetro del círculo de confusión y N la apertura del diafragma (número f).

Así pues, la distancia hiperfocal aumenta con la distancia focal f (f más grande), cuando el círculo de confusión disminuye (c más pequeño, o sea, te haces más exigente en el criterio de nitidez) y cuando abrimos el diafragma (número f más pequeño).

En la práctica, como $$f<<D_h$$, la expresión que se usa es:

Si te van las matemáticas te ves el vídeo de arriba entero. Si no, quédate con las relaciones que te he dicho y mira en el vídeo la parte de demostración con fotos.

Lo importante es que recuerdes que:

• Si doblas el número f (pasas de f/4 a f/8) la hiperfocal se reduce a la mitad.
• Si te haces la mitad de exigente en tu criterio de nitidez (pasas de un círculo de confusión de 15 a 30 micras), la hiperfocal se reduce a la mitad.
• Si divides por dos la distancia focal (pasas de 40 a 20 mm, más angular), la hiperfocal se reduce una cuarta parte (no la mitad).

Y las relaciones inversas.

Lo mismo que jugando con el tiempo de exposición, diafragma e ISO puedes conseguir muchas combinaciones que obtienen la misma exposición, jugando con la distancia focal, el diafragma y el criterio de nitidez puedes obtener muchas combinaciones con la misma hiperfocal.

Hay varias formas de calcular la distancia hiperfocal (de fácil a difícil; de más tecnológico a menos tecnológico):

• Usar una aplicación en el móvil que la calcule. Hay multitud de calculadoras de profundidad de campo para móviles. !Hasta yo tengo una! Basta con instalarla en el móvil y saber usarla. Pros: siempre viaja con tu móvil. Cons: siempre viaja con el móvil (no batería, olvido, reflejo del Sol, usabilidad, etc).
• Usar una calculadora online. La  versión para escritorio de la calculadora de profundidad de campo para el móvil. No te veo cargando un ordenador hasta lo alto de una montaña para hacer un paisaje. Y aunque lo hagas, !no tienes internet!
• Usar tablas de hiperfocales.  Cambio de tecnología. Electrónica por papel, con sus pros y cons. No se te acabará la batería, pero se te mojarán, arrugarán, ...
• Usar el cerebro. Sin duda la tecnología más probada a lo largo de los tiempos. Pros: siempre la llevas encima (no como la app, que viaja con el móvil, que no es lo mismo que viajar siempre contigo, aunque para muchos parezca lo mismo). Se te mojará y arrugará como el papel, pero seguirá funcionando (más o menos).

Cálculo de cabeza de la distancia hiperfocal

Bastará con que recuerdes el número 18 si usas un sensor APS-C o el 28 si tu cámara es full frame. Cuando utilices una distancia focal y un diafragma (número f) ese número, tu hiperfocal será un metro. Así de fácil. Por ejemplo: sensor APS-C, focal = 18 mm, f/18, hiperfocal = 1 metro.

Fíjate que si haces paisajes, esas focales son valores típicos (por ejemplo, el típico kit sensor APS-C + lente 18-55 mm ).

En el caso del diafragma lo normal es que uses números menores; no obstante, puede que alguna vez tengas que usar un f/22, pero no te aconsejo ir más allá (en el hipotético caso que tu objetivo tuviese un número f todavía más alto), salvo que quieras morir de difracción.

A partir de ahí piensa un poco aplicando estas simples reglas:

• Cada vez que multipliques (dividas) por dos la focal, la hiperfocal se multiplica (divide) por cuatro.
• Cada vez que dividas por dos el diafragma, la hiperfocal se multiplica por dos.

Ejemplo con sensor full frame

Recuerda que cuando la focal es 28 mm y el diafragma un f/28, la hiperfocal es 1 metro.

Estás fotografiando un paisaje espectacular. Vas a usar tu objetivo de focal fija de 14 mm top notch.

Decides rellenar el primer término con una flor que está a 1 metro. Enfocas a la flor, que es donde quieres máxima nitidez.

Como además quieres que la profundidad de campo llegue hasta infinito, necesitas que la hiperfocal sea 1 metro.

De regalo te llevarás un poco de profundidad de campo por delante (los objetos entre medio y 1 metro también saldrán aceptablemente nítidos en la foto).

!Pero has cambiado la focal! Estás usando 14 mm en vez de 28 mm. Como has dividido por 2 la distancia focal, la hiperfocal se ha dividido por 4.

Así que necesitas cambiar el diafragma para compensar ese factor. ¿Qué número f necesitas para que la hiperfocal siga siendo 1 metro?

Como cada vez que divides por 2 el número f la hiperfocal se multiplica por 2, deberás dividir el diafragma por 4; es decir, el diafragma que necesitas es un f/7 (7=28/4).

Resumiendo, focal 14 mm y f/7 también dan 1 metro de hiperfocal (para una full frame).

Ejemplo con sensor APS-C

Misma escena de antes pero tu sensor es APS-C y además tu objetivo es el típico 18-55 mm. Así que la focal ahora es 18 mm (no puedes hacer más angular con ese objetivo).

En este caso, decides enfocar a una roca que está a 2 metros (te gustan más las piedras que las flores).

Así que la hiperfocal ahora es 2 metros; la profundidad de campo irá desde 1 metro (la flor) hasta infinito. Fíjate que ahora la flor también saldrá aceptablemente nítida, pero la máxima nitidez está en la roca, que es donde has enfocado.

¿Qué diafragma necesitas?

Como necesitas multiplicar por dos la hiperfocal (recuerda que cuando focal = 18 mm y diafragma = f/18, la hiperfocal = 1 metro), bastará con usar un número f la mitad.

Es decir, en vez de f/18, un f/9. Así de fácil.

En los ejemplos anteriores hemos supuesto conocida la distancia hiperfocal y hemos explicado cómo obtener la combinación focal/diafragma para conseguir esa hiperfocal.

Sin embargo, casi todos lo fotógrafos utilizan otro método. Meten los datos que les pide la calculadora de profundidad de campo (cámara, focal y diafragma), y obtienen la hiperfocal, es decir, la distancia a la que deben colocarse del objeto al que quieren enfocar para que el fondo también se vea aceptablemente nítido.

Vamos a ver estas dos formas de usar el concepto de hiperfocal, con sus ventajas e inconvenientes.

Conoces la hiperfocal y focal; cálculo del diafragma

• Estás en una escena (típicamente un paisaje, algo que requiere profundidad de campo infinita por detrás) y buscas algún elemento en primer término para rellenar la foto (normalmente se usa un angular para captar mayor ángulo de visión, con lo que los objetos salen más pequeños y necesitas algo en primer término para "llenar" la foto).
• Una vez localizado ese elemento, ajustas la composisión (te mueves un poco hasta que queda como más te gusta) y ya tienes la foto lista. Al final de este proceso ya tendrás claro qué focal estás usando (suponiendo que tu objetivo sea zoom y puedas cambiar la focal, claro).
• A continuación, enfocas a ese primer elemento, para que tenga la máxima nitidez en la foto; es decir, fijas la distancia de enfoque (enfoque manual, autofocus, como quieras).
• Ahora tienes que ajustar el diafragma para que el fondo salga aceptablemente nítido. Es decir, tienes que averiguar qué número f necesitas para que la distancia de enfoque (la distancia al primer elemento) sea la hiperfocal.
• Para ello, basta con que en la calculadora (ya sea en el móvil o en tu cabeza) introduzcas la focal y el círculo de confusión (este valor se introduce implícitamente cuando eliges el tipo de cámara, el 18 o 28 de antes), y cambies el diafragma hasta que veas que la hiperfocal coincide con el valor deseado.

Conoces diafragma y focal; cálculo de la hiperfocal

• Eliges la focal, diafragma y cámara.
• Introduces esos valores en la calculadora (!no hace falta que metas la distancia de enfoque! estás calculando precisamente eso, la distancia de enfoque que en este caso es la hiperfocal; si ves un tutorial de hiperfocal donde te dicen que para calcularla hay que meter la distancia de enfoque sal corriendo de ahí).
• Te da como resultado la hiperfocal.
• Colocamos la cámara a esa distancia del elemento en primer término donde vamos a enfocar.

Obviamente, los dos métodos dan los mismos valores. Simplemente son formas distintas de trabajar. Pero es importante que entiendas que al final se trata de una ecuación matemática, donde puedes despejar la variable que te interese si conoces el resto de valores. 

En ambos casos, lo que sí sueles conocer es la distancia focal, pues es el factor que determina el ángulo de visión y por tanto la composición que has elegido.

Es decir, hay dos formas de usar la hiperfocal, cada una con sus problemas:

• Conoces la focal y la distancia hiperfocal y calculas el diafragma que necesitas. Problema: puede que obtengas un diafragma inexistente en tu objetivo (f/45, por ejemplo) o que el valor obtenido produzca difracción y tus fotos pierdan nitidez.
• Conoces la focal y el diafragma y calculas la distancia hiperfocal. Problema: puede que tengas que moverte y con ello cambiar la composición.

Independientemente del método que sigas (obviamente producen la misma foto), lo que tienes que hacer es enfocar a la distancia hiperfocal, y colocar la cámara a esa distancia del elemento en primer término donde vas a conseguir la máxima nitidez (hablando con propiedad, el único elemento en la foto que va a estar realmente enfocado).

Pero, ¿qué pasa si enfocas más lejos de la distancia hiperfocal?

Por detrás no pasa nada, pues siempre que enfoques a la distancia hiperfocal o más lejos, la profundidad de campo por detrás llegará hasta infinito.

Pero por delante perderás profundidad de campo (ya es cosa tuya saber si eso es importante o no para tu foto).

Veamos otro caso que suele ocurrir. Por ejemplo, imagina que con un f/4.5 consigues una hiperfocal de 1 metro y te colocas a esa distancia del elemento en primer término (donde vas a enfocar, es decir, distancia de enfoque = distancia hiperfocal).

Pero tú sabes que tu objetivo tiene mayor nitidez a f/9. Así que prefieres usar f/9 sin cambiar la distancia de enfoque y sin mover la cámara del sitio (misma composición).

¿Qué ha pasado? Al cerrar un paso el diafragma, la hiperfocal se ha reducido a la mitad (50 centímetros). Sin embargo, tú sigues enfocando a 1 metro. En este caso no pasa nada; al revés, todavía estás ganando algo de profundidad de campo por delante. Es cierto que si enfocases a 50 centímetros obtendrías la máxima profundidad de campo posible (de 25 centímetros hasta infinito), pero esa NO es la foto que tú quieres (quieres máxima nitidez a 1 metro).

Es el momento de sacarle partido a esta idea.

¿Qué pasa si por delante de ese primer elemento donde estás enfocando también hay más objetos que quieres que salgan aceptablemente nítidos?

Lo más intuitivo es pensar: "No pasa nada, me alejo y hago que ese primer elemento por delante que quiero que se vea aceptablemente nítido coincida con la mitad de la hiperfocal".

Si haces eso, efectivamente, como sigues enfocando a la hiperfocal, la profundidad de campo irá desde la mitad de la hiperfocal (tu elemento más delantero) hasta infinito. Problema de profundidad de campo resuelto.

Sí, pero tienes dos efectos colaterales.

El primero es que has movido de cámara de sitio, así que ya no tienes la misma perspectiva.

Al alejarte y mantener la focal, estarás captando más campo de visión (el ángulo de visión es el mismo, pero ahora sacarás más campo de visión en la foto). Así que puede que esa nueva foto ya no te guste tanto.

El segundo efecto es que al alejarte pero mantener la distancia de enfoque (sigues enfocando a la hiperfocal, y ésta no cambia pues no has cambiado el diafragma ni la focal ni tu criterio de nitidez), ya no estás enfocando al objeto donde quieres máxima nitidez.

Tu foto tiene la profundidad de campo deseada, pero el plano enfocado no coincide con donde tú quieres.

Lo que tú quieres es que el objeto que está más cerca también salga aceptablemente nítido, pero:

• No quieres cambiar la perspectiva: te ha costado mucho conseguir esa composición y ESA es la foto que quieres. Así que no vale mover la cámara para ganar profundidad de campo por delante, porque entonces estás cambiando la perspectiva.
• No quieres cambiar el punto de enfoque. Quieres máxima nitidez en ESE objeto. Así que no vale mover la cámara alejándote porque entonces el punto de enfoque cambiará (al no cambiar la distancia de enfoque y alejar la cámara, el enfoque ya no cae sobre el objeto que quieres máxima nitidez, sino en un punto  más cercano).

Resumiendo, quieres ganar profundidad de campo por delante pero sin mover la cámara ni cambiar la distancia de enfoque.

¿Qué puedes hacer?

Como no puedes tocar la focal (no quieres cambiar la composición), lo único que te queda es cerrar el diafragma. Al cerrar el diafragma, la hiperfocal se reduce.

Pero, recuerda: !no enfocas a la nueva hiperfocal! Tu distancia no enfoque no cambia, porque quieres máxima nitidez en el objeto de antes. En este caso, estás enfocando más lejos de la nueva distancia hiperfocal.

La ventaja de reducir la hiperfocal es que ganas profundidad de campo por delante. Por detrás no hay problema: siempre que enfoques a la hiperfocal o más lejos (como en este caso), la profundidad de campo por detrás llegará hasta infinito.

Cuanto más cerca tengas el objeto que quieras que se vea aceptablemente nítido también, más tendrás que cerrar el diafragma. Así que, de nuevo, en muchos casos tendrás que decidir entre difracción o tener que mover la cámara y alejarte.