Curso Fundamentos Ópticos en Fotografía
Resumen
El factor de magnificación (o magnificación a secas) indica la relación de tamaños entre la imagen y el objeto.
Por ejemplo, una magnificación 1:2 indica que la imagen que se obtiene tiene la mitad de tamaño que el objeto real.
Es un término que se usa mucho en Fotografía macro.
Magnificación de la lente
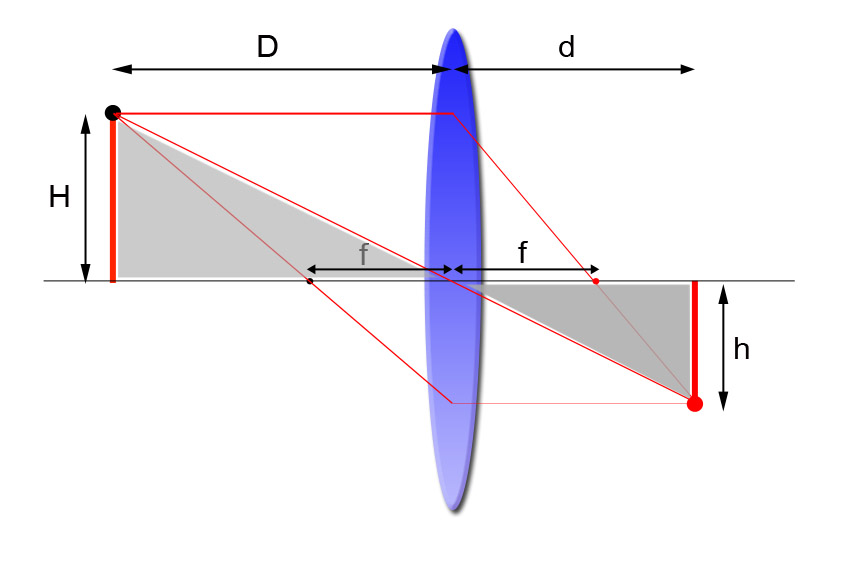
La distancia a la que se forma la imagen se obtiene a partir de la distancia focal y la distancia de enfoque mediante la ecuación de lente, donde f es la distancia focal, D la distancia de enfoque y d la distancia a la que se forma la imagen:
\frac{1}{f} = \frac{1}{d} +\frac{1}{D}
La magnificación de la lente se define como la relación entre el tamaño de la imagen y el tamaño del objeto y se representa con una m. Siguiendo con la notación de la figura 1:
m = \frac{h}{H}
La relación \frac{h}{H} es la misma que la que guardan los lados D y d, pues los triángulos grises son semejantes. Así pues, m se puede expresar como relación de tamaños entre la imagen y el objeto, o como relación entre distancia de la imagen y distancia de enfoque:
m = \frac{h}{H} = \frac{d}{D}
Usando la ecuación de la lente, el factor de magnificación también se puede expresar en función de la distancia focal f y la distancia de enfoque D:
m = \frac{f}{{D - f}}
o en función de la distancia de la imagen:
m = \frac{d}{f} - 1
Como ves, el factor de magnificación es otra forma de dar la misma información que la ecuación de la lente; simplemente es más útil cuando lo que nos interesa es saber la relación de tamaños entre la imagen y el objeto, como suele ser el caso en fotografía macro.
El factor de magnificación es un número relativo porque relaciona dos distancias.
Por ejemplo, un objetivo macro típico verás que indica 1:1. Esto significa que el objetivo es capaz de obtener imágenes del mismo tamaño que el objeto; si haces la foto de una hormiga de 5 mm, la imagen de la hormiga invertida en el sensor ocupará 5 mm.
Otra forma de verlo: la distancia a la que se forma la imagen es la misma que la distancia de enfoque.
Volver al menú principal del tutorial Fundamentos Ópticos en Fotografía

Después de buscar un montón de sitios donde expliquen la relación entre focales, magnificación, macro… he llegado a tu tutorial, Y ME ENCANTA. Muchas gracias!!
Dado el siguiente gráfico: M—f’—l—f—S,
que representa el «motivo a enfocar» (M), la «lente» (l), el «foco de la lente» (f) y el «sensor» o «plano de enfoque» (S), tengo una duda, pues a la luz de tus explicaciones, se desprende que:
– Para tener magnificación 1:1, se necesita que el «motivo a enfocar» esté -respecto el sensor-, a 4x la «distancia focal de la lente» (lf);
– Para una lente de «distancia focal» (lf) 40mm, si se pretende una magnificación 1:1, se necesita una distancia entre el «motivo» y «sensor» (MS) de 160mm.
Así las cosas, y con la distancia de enfoque mínima del Nikkor 40mm macro, que dice ser de 163mm, no se puede obtener una magnificación de 1:1, pues el motivo está más alejado de los 160mm necesarios;
He hecho los cálculos para esta distancia, y parece que la magnificación para esta lente está entorno al 1:1.3
Debo entender este hecho como que:
a) los fabricantes «dulcifican» las propiedades de sus objetivos,
b) el modelo de «lente delgada» no vale para confirmar estos datos, debiendo aplicarse el modelo de «lente gruesa»,
c) he entendido mal toda su explicaión, y mejor que me la relea de nuevo porque he pasado cosas por alto.
Datos del Nikkor 40mm macro, en:
http://www.nikonusa.com/en/Nikon-Products/Product/Camera-Lenses/2200/AF-S-DX-Micro-NIKKOR-40mm-f%252F2.8G.html#
Muchas gracias por poner a nuestra disposición todo su trabajo!!
tratas muchas cosas 🙂
1. la distancia de enfoque que marca el objetivo es desde el plano del sensor, no desde la lente. Así que ya puedes olvidarte de hacer ningún cálculo porque:
2. Efectivamente el modelo correcto es el de lente gruesa y necesitas saber dónde están los puntos nodales porque las distancias en las fórmulas se miden desde ahí.
3. los diseños de objetivos son mundos ignotos; en angulares utilizan técnicas para que a pesar de usar focales muy pequeñas les quepa el espejo entre lente y sensor; y para los teles al revés. el efecto curioso es que puede que tengas los puntos nodales fuera del objetivo.
4. por no hablar de las focales que marcan los fabricantes y que suelen tener cierta tolerancia; si tienes dos objetivos con la misma focal haz fotos con el mismo cuerpo y puede que veas que el ángulo de visión no es exactamente igual
así que en el caso de macro lo mejor es utilizar la escala de magnificación que marca el objetivo y despejar de las fórmuals que relacionan las variables
Hola, un lente que dice ser 1:4 es indicado para macro?
Muchas gracias
Normalmente el término macro se reserva para 1:1 o más. De todas formas lo de menos es cómo se llama. Lo importante es si es lo que necesitas. 1:4, o sea, una magnificación de 0.25, simplemente dice que algo que mide 1 cm en la realidad aparecerá en la imagen obtenida por el objetivo como 2.5 mm (lo que captes dependerá del tamaño del sensor). Hay formas de aumentar la magnificación conectando otras cosas al objetivo si con 1:4 no tienes bastante (tubos, lentes, etc)
tengo un lente con una magnificacion de 1:2.3/50mm, que magnificacion en terminos de X tendria?
1/2.3 = 0.43 1 cm de la realidad te quedari como 4,3 mm grabado en el sensor
Tengo una confusión enorme y me gustaría que me ayudaran.
Uniendo dos lentes de acercamiento Raynox de +8 y +4.8 y colocandolo frente a un objetivo macro Laowa de 100mm y a 1:1, la magnificación de imagen real resultante cual seria?
Saludos, quiero comprar un lente macro que sea 1:1 pero no se donde puedo encontrar esa información o como la escriben para estar seguro al comprar
he mirado este lente (Canon – RF100mm F2.8 L MACRO IS USM Telephoto Lens for EOS R-Series)
que dicen es macro con magnificaron 1:1 pero no veo que lo diga por ningún lado
agradeceria mucho la ayuda de ustedes
gracias
Hola. Los fabricantes especifican la magnificación normalmente con una x. Por ejemplo,https://www.canon-europe.com/lenses/rf-100mm-f2-8l-macro-is-usm/ es un 1.2x, es decir más del 1x que significa mismo tamaño real que en el sensor