Curso Fundamentos Ópticos en Fotografía
Resumen
Obtenemos la ecuación que relaciona la distancia focal de una lente f con la distancia de enfoque D y la distancia a la que se forma la imagen d.
Se llama ecuación de la lente y es:
\frac{1}{f} =\frac{1}{d} +\frac{1}{D}
Ecuación de la lente
En artículos anteriores hemos aprendido a calcular las imágenes. Además has visto cómo la distancia de enfoque influye en la distancia a la que se forma la imagen.
Así que, ¿existe alguna fórmula que me permita obtener la distancia a la que se forma la imagen conocida la distancia focal y la distancia de enfoque?
Sí. Se llama ecuación de la lente, y viene dada por:
\frac{1}{f} =\frac{1}{d} +\frac{1}{D}
donde f es la distancia focal de la lente, d la distancia a la que se forma la imagen y D la distancia a la que se encuentra el objeto (distancia de enfoque).
Relación entre distancia de enfoque, distancia de la imagen y distancia focal
Fíjate que cuando la distancia de enfoque es infinito, D tiende a infinito, y nos queda </span>\frac{1}{f} = \frac{1}{d} . Es decir, la imagen se forma a la distancia focal f=d, coincidiendo con lo que habíamos obtenido geométricamente en el artículo anterior.
Por otra parte, si el objeto está a D=2f, despejando obtenemos d=2f, que también coincide con lo que habíamos calculado antes gráficamente.
Resumiendo, la ecuación de una lente nos da la distancia a la que se forma la imagen en función de la distancia a la que enfocamos y la distancia focal de la lente.
Esa distancia está muy cercana a la distancia focal para el caso de objetos lejanos. Este es el caso típico en Fotografía.
Si la distancia focal es de 50 mm, ¡tan sólo 5 cm!, basta con que enfoques a 5 metros para que ya tengas una relación 100:1 de distancias. ¡Imagínate cuando enfocas a una montaña a varios kilómetros o a la Luna que está a 384.000 km!
Pero existe un tipo de Fotografía donde esto no es así, donde la distancia a la que se encuentra el objeto es muy pequeña: la Macrofotografía.
Consiste en hacer fotos de objetos muy pequeños; para ello, es necesario que nos acerquemos mucho al objeto, con lo que ya no podemos suponer que la distancia de enfoque es muy superior a la distancia focal.
Ten en cuenta que cualquier foto que hagas donde la distancia al objeto sea del orden de la distancia focal, la suposición que la imagen se forma cerca de la distancia focal es falsa.
Como ves, cuando fotografías objetos cercanos todo se complica, pues las imágenes ya no se forman cerca de la distancia focal. Tan es así, que en Macrofotografía utilizan otro parámetro además de la distancia focal para indicar las características de un objetivo macro: el factor de magnificación.
Sin embargo, el factor de magnificación es un parámetro fácilmente calculable para cualquier lente, aunque en la práctica sólo se usa para los objetivos macro.
Demostración
Para los que quieran ver cómo se obtiene la ecuación de la lente. Si no te interesan mucho los detalles matemáticos, salta a la siguiente lección del tutorial.
Para ello necesitamos usar las tres reglas de los rayos y un poco de Matemáticas.
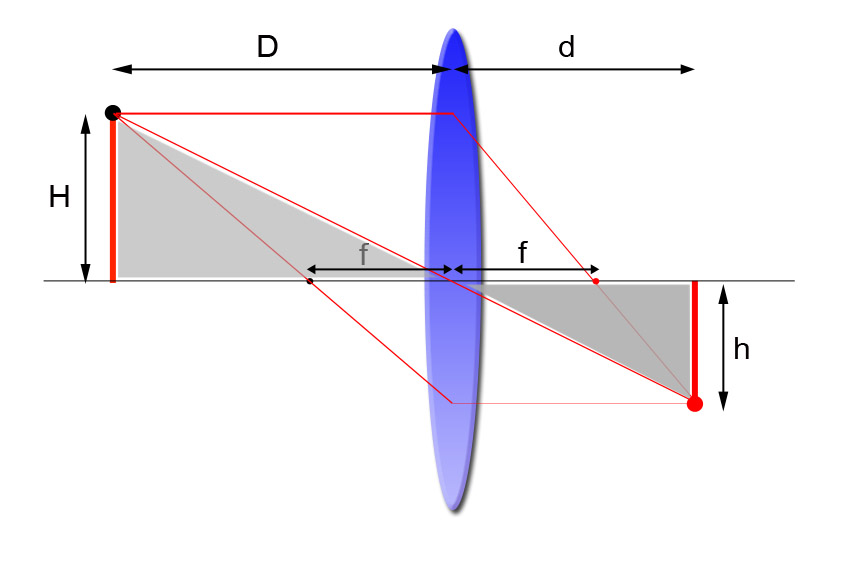
En la figura 1 representamos los tres rayos de dichas reglas. Indicamos los siguientes valores: el objeto es de tamaño H, la imagen de tamaño h, la distancia de enfoque es D, la distancia desde la lente hasta la imagen es d. Además, conocemos la distancia focal f.
El objetivo es obtener la ecuación que relaciona estas distancias. A esa ecuación se le llama ecuación de lente y se obtiene a partir del estudio geométrico de la figura 1.
En la figura 1 hemos indicado en gris dos triángulos semejantes (fíjate que tienen los mismos ángulos, pero el de la zona imagen es más pequeño y está girado del revés). De dichos triángulos podemos sacar la siguiente relación:
</span>\frac{H}{D} =\frac{h}{d}
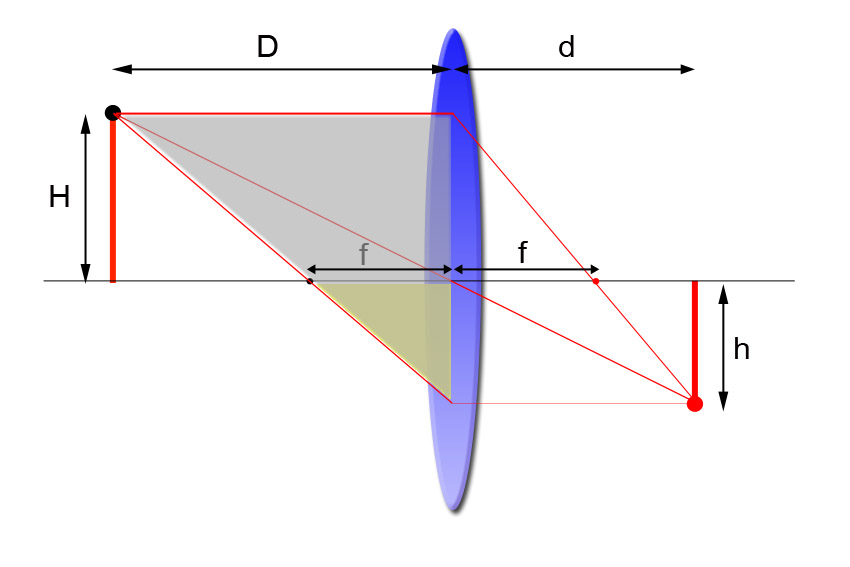
Además, hay otros dos triángulos semejantes en la figura 1; en este caso los marcamos como amarillo y gris para facilitar su localización, pues el amarillo está incluido en el gris (ver figura 2):
La relación entre lados de dichos triángulos es:
</span>\frac{h}{f} = \frac{{h + H}}{D}
Compruébalo tú mismo; fíjate que en el triángulo gris la altura del cateto vertical es la suma de H más la altura del cateto del triángulo amarillo, que es h. Esta ecuación se puede expresar también como:
</span>\frac{H}{D} = \frac{h}{f} - \frac{h}{D}
Así pues, tenemos dos ecuaciones:
</span>\frac{H}{D} = \frac{h}{d} <span style="color: #000000;">
</span>\frac{H}{D} = \frac{h}{f} - \frac{h}{D}
donde f es conocido. Sustituyendo la primera ecuación en la segunda, obtenemos:
</span>\frac{h}{f} - \frac{h}{D} = \frac{h}{d}
Si dividimos en ambos lados de la igualdad por h, llegamos a la ecuación de una lente delgada:
\frac{1}{f} =\frac{1}{d} +\frac{1}{D}
Volver al menú principal del tutorial Fundamentos Ópticos en Fotografía

MAGNÍFICO
es excelente aporte mil gracias.
Hola Jorge,
Gracias por tu blog. He estado usando la ecuacion de más arriba.
Necesito una cámara (o varias cámaras) y un objetivo (o varios objetivos) con los que pueda detectar un objeto de tamaño 20x20cm a una anchura de 15m y a una distancia de 1000m.
Una combinación seria utilizar por ejemplo una camara con un sensor de formato de 1/3″ y necesitaría un objetivo con una distancia focal de unos 410 mm. Me resulta raro, saber que por los 1000m se reduce drásticamente el tamaño dl sensor de la camara. Mi pregunta, es posible ocupar una camara Full frame o 4/3″ o APS o de tamaño de formato similar con una lente que me pueda fotografiar una objeto de tamaño 20cmx2cm a 1000m?
hola. disculpa el retraso. No me queda clara del todo la pregunta. ¿Quieres fotografiar un objeto de tamaño 0.2×0.2 m a una distancia de 1000m? Lo veo imposible. Lo primero que necesitas saber es la magnificación que necesitas: imagina que tu sensor mide X (para simplificar piensa en una sola dimensión, por ejemplo el ancho de sensor; para un full frame por ejemplo es 36 mm); ¿cuánto quieres que ocupe tu objeto de esos 36 mm? o ¿lo que quieres es que los 15 m sean tu campo de visión?, es decir, que esos 15 m se conviertan en 36 mm en tu sensor (si es así ya puedes calcular la magnificación m= 0.0024 y con ese dato y la distancia de enfoque 1000 m despejar la focal f=2394 mm, una barbaridad imposible de conseguir; puedes reducirla usando un sensor más pequeño, pero esa focal tampoco existe en objetivos para 4/3′ (para que te hagas una idea un iphone 12 lleva una focal de 5.1mm, que es como si usases un objetivo de 26mm en full frame (mismo ángulo de visión). Ya no te digo nada si quieres fotografiar algo de 20 cm a 1 km de distancia!!! Resumiendo, no hay cámara/objetivo que te consiga esa resolución angular
Muy buena aclaración, Jorge!
Hola,
Hago astrofotografía de cielo profundo… Quiero hacer fotos de campo muy amplio y para ello quiero conectar la cámara dedicada ( ASI ZWO 183 MC Pro ) a un objetivo Nikon 35 mm 1.8.
Para poder hace foco lo hago directamente sobre las estrellas de noche… D la distància al objeto tiende al infinito con lo que la imagen se forma teóricamente a la distancia de la focal, 35 mm…
Pero no consigo hacer foco… Haciendo ensayo y error lo consigo a unos 42 mm … así q voy a comprar anillos extensores para poder unir cámara y objetivo y que queden a 42 mm .. pero no entiendo porque no se cumple en mi caso la fórmula… Entiendo q se me escapa algo importante… Mucha muchas gracias
hola. Cuando enfocas a infinito la imagen siempre se forma a la distancia focal. La pregunta clave es: ¿desde dónde mides los 35 mm? En el modelo de lente delgada está claro que al haber solo 1 lente todas las distancias se miden respecto a ella. Pero un objetivo tiene muchas lentes, así que este modelo no sirve. Un objetivo real se modela con una lente gruesa y la distancia focal se mide desde el segundo plano principal. SOn conceptos técnicos más avanzados que en breve crearé un nuevo tutorial para explicarlo todo (de hecho justo estoy acabando un libro sobre el tema porque mucha gente tiene dudas como la tuya o similares). Al no usar la montura de Nikon, me tremo que el problema lo tengas ahí, que el objetivo cree la imagen a la distancia de registro de la montura de Nikon. Si ese es el problema, debes añadir lo que sea para que ambas distancias coincidan y entonces sí tendrás el plano imagen sobre el sensor.