13. El confuso círculo de confusión

Curso Fundamentos Ópticos en Fotografía

Resumen

El círculo de confusión es un valor clave para determinar la profundidad de campo.

Repasamos en este artículo diferentes criterios para establecer su valor.

---

El círculo de confusión

La profundidad de campo depende del diámetro máximo del círculo de confusión (CoC en adelante) que aparece en la imagen que registra el sensor.

Ese diámetro máximo es aquél que hace que a la vista el círculo parezca un punto.

¿De qué depende que un círculo se vea como un punto o como un círculo?

Básicamente de dos factores: la agudeza visual (detectas círculos más pequeños cuanta mayor agudeza tengas) y la distancia de observación (detectas círculos más pequeños cuanto más cerca del círculo estés).

Y aquí comienzan los problemas. Según los valores de agudeza visual y distancia de observación que consideres el CoC será uno u otro.

Para complicarlo más, la agudeza visual también depende de muchos factores, por ejemplo la edad o las condiciones de visualización: en un entorno mal iluminado la agudeza visual baja considerablemente (por ejemplo, en condiciones de muy poca luz no distinguimos los colores).

Agudeza visual

La agudeza visual es el mínimo ángulo que el ojo humano es capaz de distinguir.

No existe un valor universal de agudeza visual. Es un concepto que depende de muchos factores, con lo que se encuentran diferentes valores en la literatura.

Se suele expresar de dos formas: o cómo ángulo, o como pares de líneas por mm que somos capaces de distinguir a una cierta distancia (otra forma de definir un ángulo).

Por ejemplo, un valor típico es el siguiente: a 25 cm de distancia un ojo humano puede distinguir hasta 5 pares de líneas por mm (lp/mm). Lo representamos en la figura 1.

Figura 1. Resolución 5 lp/mm

Consta de 5 pares de líneas verticales (negro/blanco).

Imagina que las 10 líneas juntas miden 1 mm de ancho, es decir, cada par de líneas mide 0.2 mm.

Si las miras de cerca las distinguirás. A medida que te vayas alejando llegará un punto donde no serás capaz de distinguirlas: en vez de rayas negras y blancas verás un cuadrado gris.

Esa distancia es 25 cm.

Es decir, podemos calcular la agudeza visual como un ángulo (figura 2):

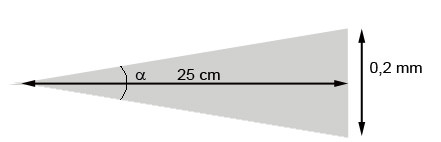
Figura 2. Agudeza visual de 5 lp/mm a 25 cm. Ángulo equivalente

Donde el ángulo se puede obtener fácilmente como:

\alpha=2\arctan \frac{{0,1}}{{250}}=0,05^\circ=2,75'

Lo de menos es el valor 2,75’ (léase 2,75 minutos de arco, donde un minuto de arco es 1/60 grados o 0.000291 radianes).

¿Por qué? Porque encontrarás muchos otros valores igualmente válidos puesto que se trata de un criterio subjetivo.

Por ejemplo, un valor más cercano a la realidad es el de 1’.

Si no me crees, haz tú mismo la prueba y calcula tu agudeza visual; dibuja en un papel un cuadrado blanco y otro negro de h mm de lado cada uno y empieza a separarte perpendicularmente del papel; llegará una distancia D donde no los distinguirás; verás un cuadrado gris de lado 2h mm. Sabiendo esa distancia D (en mm) y que los cuadrados miden 2h mm, puedes calcular tu agudeza visual como:

\alpha=2\arctan \frac{h}{D}

Por ejemplo, si los cuadrados son de 1 cm de lado y dejas de distinguirlos a 25 m de distancia, tu agudeza visual es la misma de antes porque:

\alpha=2\arctan \frac{1}{{2500}}=2,75'

Resumiendo, el criterio útil que debería tenerse en cuenta para el cálculo de la profundidad de campo es el ángulo de agudeza visual, porque nos da la relación entre el CoC y la distancia de observación, con lo que si aumentamos la distancia el doble sabemos que podemos ampliar el CoC el doble sin que el ojo lo note.

Tamaño máximo del círculo de confusión

En Fotografía nos gusta más usar el confuso CoC porque la fórmula de profundidad de campo utiliza el tamaño del CoC sobre el sensor como un dato.

Y para calcular el tamaño máximo de un círculo que el ojo no sea capaz de distinguir de un punto en una foto o en el sensor necesitamos saber la distancia de observación.

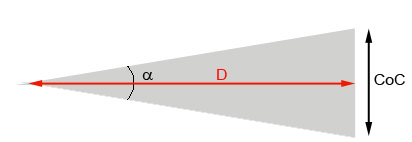
Figura 3. Cálculo del CoC en función de la distancia de observación

De la figura 3 podemos obtener la siguiente relación:

\tan\frac{\alpha }{2} = \frac{{CoC/2}}{D}

Puesto que el ángulo α es muy pequeño (en la figura el ángulo está exagerado para facilitar la interpretación), podemos sustituir la tangente por su ángulo (en radianes) \(\tan\frac{\alpha }{2}=\frac{\alpha }{2} [/katex].

Finalmente, despejamos y obtenemos el valor del tamaño máximo del CoC:

CoC = 2D\tan\frac{\alpha }{2} = 2D\frac{\alpha }{2} = D\alpha

El resultado nos dice que el CoC máximo que veremos como un punto depende de la agudeza visual α y de la distancia a la que observemos D.

Si la agudeza es muy buena (α pequeño), CoC será muy pequeño; si la distancia de observación es muy grande (D grande), CoC será muy grande.

La fórmula coincide con nuestra experiencia visual: un círculo muy grande visto desde muy lejos parece un punto (enfocado), y un punto muy pequeño observado desde muy cerca puede parecer un círculo (desenfocado).

Esto significa que cuando leas por ahí que el diámetro del CoC es 0,2 mm no significa nada.

Se puede obtener el mismo CoC máximo si observas la foto desde muy lejos (D grande) con un ojo con mucha agudeza (α pequeño) que si la observas desde muy cerca (D pequeño) con un ojo con poca agudeza (α grande).

Ya sabemos cómo se mide la agudeza visual. Es hora de analizar la distancia de observación.

Distancia de observación

¿Cuál es esa distancia de observación típica?

Al igual que ocurrió con la agudeza visual, tenemos que fijar un criterio.

Un criterio muy usado dice que la distancia habitual a la que observamos una foto es aquella que el ángulo de visión diagonal es aproximadamente 60°.

Por ejemplo, para una foto 20×25 cm (diagonal 30 cm), si te sitúas a 25 cm el ángulo de visión diagonal es aproximadamente 60°. Gráficamente:

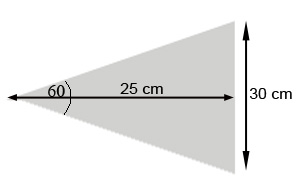
Figura 4. Ángulo de visión 60°

Donde se cumple que \arctan \frac{{15}}{{25}}=30^\circ .

Ahora que ya sabemos que la distancia de observación es D=25 cm, podemos calcular el CoC máximo dado un ángulo de agudeza visual de 2,75 minutos de arco (recuerda que hay que pasarlo a radianes):

CoC = D \cdot \alpha=25 \cdot \frac{{2.75}}{{60}} \cdot \frac{\pi }{{180}}=0,02 cm=0,2mm

Obviamente el resultado es el mismo que antes pues estamos a la misma distancia 25 cm y hemos supuesto la misma agudeza visual.

¿Qué pasa si la foto que estamos viendo es más pequeña, por ejemplo una copia 10×15 cm?

Pues que la distancia a la que veremos la foto disminuirá. Dicho de otra forma, como el ángulo de visión es constante, podemos obtener la distancia D si conocemos el tamaño de la copia (figura 5).

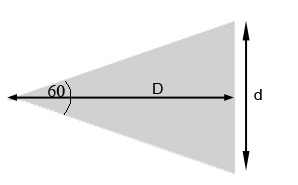
Figura 5. Distancia D a la que observar una foto de diagonal d

En la figura 5, D representa la distancia a la que hay que observar una foto cuya diagonal mide d, para que el ángulo de visión diagonal sea 60°. De la figura se deduce que:

tan30=\frac{{d/2}}{D}

Despejando, obtenemos:

D = 0,866 \cdot d

Esta ecuación nos dice a qué distancia D hay que colocarse para observar una foto cuya diagonal mida d.

Conocida esa distancia y el ángulo de agudeza visual, podemos calcular el tamaño máximo del CoC.

Por ejemplo, ¿cuál es el CoC que el ojo en una copia 10×15 cm verá como un punto y por tanto pensará que el objeto está enfocado?

Primero calculamos la diagonal d de una foto 10×15 cm:

d = \sqrt {10^2+15^2 }={\rm{1}}8{\rm{ cm}}

Luego calculamos la distancia a la que hay que observar una foto 10×15 cm para que la diagonal cubra 60° de nuestro campo de visión:

D = 0.866 \cdot d = 0.866 \cdot 18 = {\rm{15}},{\rm{6 cm}}

Conocida la distancia, obtenemos el CoC máximo tolerable en la copia 10×15 cm.

CoC = D \cdot \alpha=15,6 \cdot \frac{{2,75}}{{60}} \cdot \frac{\pi }{{180}}=0,125 mm

Es decir, cuando vea a una foto 10×15 cm a una distancia de 15,6 cm y suponiendo una agudeza visual de 2,75 minutos de arco, veré desenfocados los objetos puntuales que en la foto aparezcan como círculos de diámetro mayor a 0,125 mm.

Como era de esperar el CoC se ha hecho más pequeño que el caso de 0,2 mm pues la distancia de observación se ha hecho más pequeña y por tanto detectaremos antes los círculos (a igual agudeza visual).

Puesto que la agudeza visual y el ángulo de visión son valores que dependen del criterio elegido, nos interesa tener una fórmula donde estos valores aparezcan como parámetros.

Ecuación del círculo de confusión

De las ecuaciones anteriores, tenemos:

CoC = \frac{{d \cdot \alpha }}{{2\tan (\beta /2)}}

donde d es la diagonal de la foto, α es el ángulo de agudeza visual en radianes y β el ángulo diagonal de visión que sirve para calcular la distancia de observación.

Esta fórmula es válida para cualquier valor de d, así que podemos suponer que d es el tamaño de la diagonal del sensor.

De esta forma conseguiremos una expresión que nos dará el valor del C0C sobre el sensor y que podremos usar para calcular la profundidad de campo.

Volver al menú principal del tutorial Fundamentos Ópticos en Fotografía