8. Cálculo del ángulo de visión en función de la distancia focal y el tamaño del sensor

Curso Fundamentos Ópticos en Fotografía

Resumen

El ángulo de visión es función de la distancia focal y el tamaño del sensor; viene dado por la ecuación:

\alpha=2\arctan \frac{S}{{2f(m + 1)}}

donde α es el ángulo de visión, S el tamaño del sensor, f la distancia focal y m el factor de magnificación. Para distancias de enfoque grandes (m≈0), queda:

\alpha=2\arctan \frac{S}{{2f}}

---

Cálculo del ángulo de visión

Hemos visto cómo influye el tamaño del sensor y la distancia focal en el ángulo de visión que es capaz de abarcar una lente delgada.

Podemos obtener la expresión matemática que relaciona el ángulo de visión con la distancia focal y el tamaño del sensor.

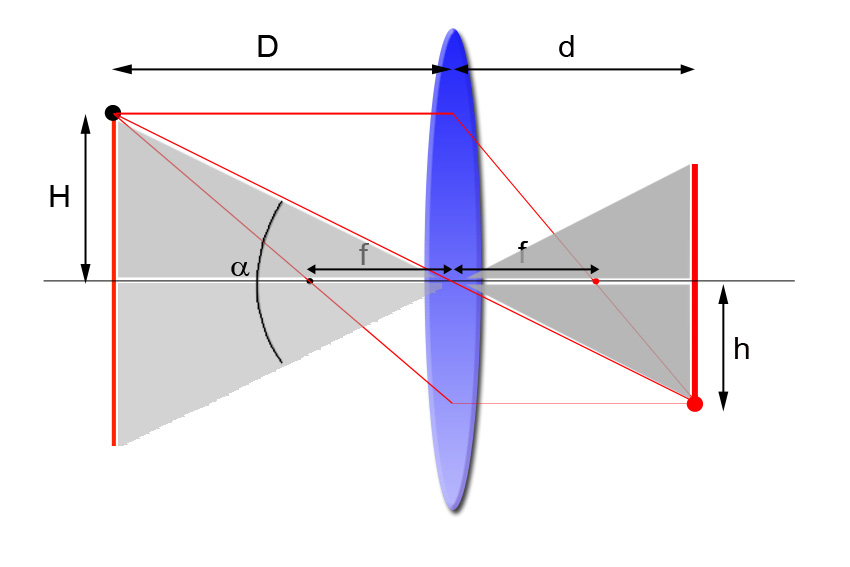
Partimos del modelo de lente delgada y representamos el objeto de mayor tamaño H que es capaz de captar el sensor, generando una imagen de tamaño h, para una lente de distancia focal f.

Por simple inspección de la figura, sabemos que:

tan \frac{\alpha }{2} = \frac{H}{D}

Despejando, obtenemos el ángulo de visión:

\alpha=2\arctan \frac{H}{D}

Los triángulos grises de la figura son semejantes. Así que dicho ángulo es el mismo que se forma en el triángulo de la zona imagen:

\alpha=2\arctan \frac{h}{d}

Cálculo del ángulo de visión para distancias de enfoque lejanas

Si D tiende a infinito, sabemos que d tiende a f (la imagen se forma a la distancia focal). Por tanto, tenemos:

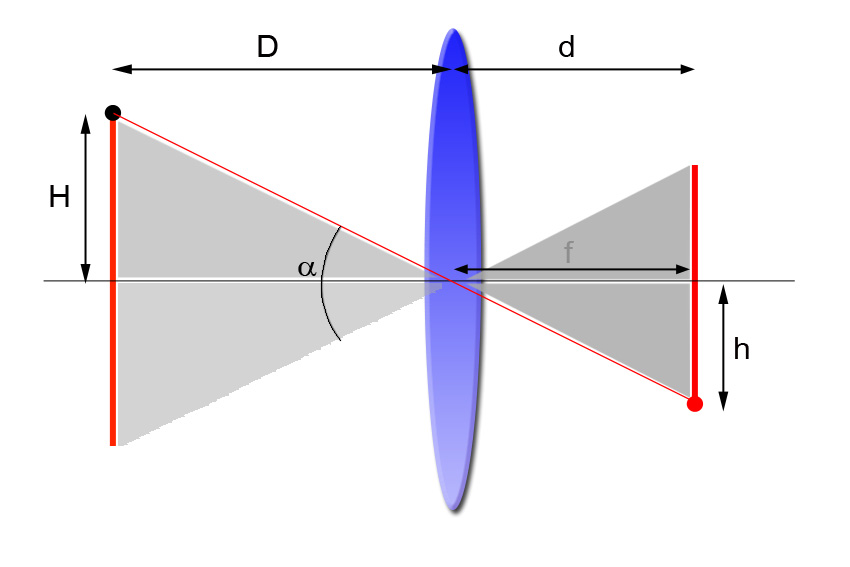
\alpha=2\arctan \frac{h}{f}

Para entenderlo gráficamente de una manera sencilla, se utiliza el modelo de cámara estenopeica (sin lente, se supone que los rayos pasan por un agujero muy pequeño sin desviarse y se forman las imágenes perfectas en la superficie del sensor), representado en la figura 2:

La ecuación del ángulo de visión se suele dar en función de la distancia focal f y el tamaño total del sensor S. Observando la figura, sabemos que el tamaño del sensor es S = 2h.

Por tanto, la expresión final queda:

\alpha=2\arctan \frac{S}{{2f}}

donde S es el tamaño del sensor y f la distancia focal. Queda claro que a mayor tamaño del sensor S, mayor ángulo y a menor distancia focal f, mayor ángulo de visión.

Como los sensores tienen diferentes dimensiones horizontal, vertical y diagonal, se habla de ángulo de visión horizontal, vertical o diagonal según incluyamos en la fórmula la dimensión horizontal, vertical o diagonal del sensor, respectivamente.

Así que cuando te digan que un objetivo tiene un ángulo de visión de 45°, averigua si están hablando del ángulo horizontal, vertical o diagonal. Normalmente suele ser el diagonal, pero asegúrate.

Por ejemplo, el sensor full frame tiene las mismas dimensiones que el negativo tradicional de 35 mm. Dichas dimensiones son: 24 x 36 mm (diagonal 43.3 mm).

Enfocando a infinito, los ángulos de visión que se obtienen para una lente de 50 mm son: 40°, 27° y 47° (horizontal, vertical, diagonal).

Se suele decir que un 50 mm es una distancia focal normal porque el ángulo de visión que produce es perceptualmente similar al que tenemos cuando observamos una foto impresa a una distancia normal.

Este es el origen de otra de las grandes confusiones en Fotografía. Antes de la fotografía digital, casi todo el mundo que hacía fotos utilizaba el mismo tipo de “sensor”, el negativo de 35 mm.

Así que nos habituamos a llamar a los objetivos por debajo de 50 mm angulares y por encima teleobjetivos, indicando que los primeros tienen mayor ángulo de visión y los segundos menor.

Pero en la actualidad, ¡hay multitud de sensores con tamaños diferentes! De hecho, casi nadie tiene una cámara full frame.

Por ejemplo, el sensor que lleva un móvil puede tener un tamaño típico 3.42×4.54 mm, es decir, unas ¡8 veces más pequeño que una full frame!

Por eso en las cámaras compactas verás que las distancias focales son mucho menores a las de una réflex; y no te digo nada si comparas las distancias focales de un móvil con las de los objetivos que usa una cámara de medio formato.

Resumiendo, la fórmula que nos da el ángulo de visión cuando enfocamos a infinito depende de la distancia focal, pero también del tamaño del sensor.

Así que es mejor que te quedes con la siguiente regla para saber lo que es una distancia focal normal (entendiendo por normal aquella que produce un efecto visual parecido al del ojo humano, es decir que tiene un ángulo de visión de unos 47 grados):

Un objetivo es normal (entendiendo por normal que genera un ángulo de visión parecido al ojo humano) cuando la distancia focal es aproximadamente igual a la diagonal del sensor.

Por ejemplo, para el full frame digital o negativo tradicional de 35 mm, unos 43 mm (muy cerca de los 47 mm teóricos y de los 50 mm que tiene el objetivo «normal» por excelencia).

A veces, en vez del ángulo de visión, se habla de campo de visión cuando se indica la dimensión física en la zona objeto que abarca la lente.

Por ejemplo, el campo de visión en la figura 2 es 2H. Pero esta medida sólo tiene sentido si además indicas la distancia de enfoque (a qué distancia están los objetos de la lente, es decir, D en dicha figura).

Todo lo visto hasta ahora es para distancias de enfoque muy lejanas. ¿Qué pasa a medida que la distancia de enfoque se reduce?

Cálculo del ángulo de visión para distancias de enfoque cercanas

La hipótesis “distancia de la imagen aproximadamente igual a la distancia focal” deja de ser cierta a medida que la distancia de enfoque se reduce.

En particular, la fórmula anterior no se puede aplicar para distancias muy cortas (del orden de la distancia focal).

Para distancias de enfoque pequeñas, la fórmula correcta es:

\alpha=2\arctan \frac{S}{{2f(m + 1)}}

que se puede obtener fácilmente de la figura 1. Si comparas esta fórmula con la aproximada de antes para distancias lejanas, la diferencia se debe al factor de magnificación m.

Las diferencias entre los ángulos de visión calculados por ambas ecuaciones son mínimas para distancias lejanas porque m suele ser muy pequeño.

Veamos un ejemplo numérico para comprobarlo: un objetivo de 50 mm en un sensor full frame.

Cuando enfocamos a infinito, la aproximación es exacta, pues m=0. Nos queda:

\alpha=2\arctan \frac{S}{{2f(m + 1)}} = 2\arctan \frac{{36}}{{2 \cdot 50}} = 40^\circ

Para una distancia de enfoque de 55 cm, el factor de magnificación ya no es cero. Lo calculamos:

m = \frac{f}{{D - f}} = \frac{{50}}{{550 - 50}} = 0.1

Como ves, no hemos elegido 55 cm casualmente, sino para que diera un factor m fácil de interpretar.

El valor obtenido quiere decir que cuando hagas una foto de un objeto de tamaño real 10 cm con un objetivo de 50 mm en una cámara full frame, la imagen registrada (invertida) será de tamaño 1 cm.

Calculamos el ángulo de visión de la cámara a esa distancia:

\alpha=2\arctan \frac{S}{{2f(m + 1)}} = 2\arctan \frac{{36}}{{2 \cdot 50(0.1 + 1)}} = 36^\circ

El ángulo de visión se ha reducido tan sólo 4°; no parece mucho si tenemos en cuenta que hemos acercado el objeto de infinito a tan sólo 55 cm de nuestra lente.

Para un objetivo de 50 mm macro con un factor de magnificación m=1 (distancia de enfoque D=10 cm), nos quedaría:

\alpha=2\arctan \frac{S}{{2f(m + 1)}} = 2\arctan \frac{{36}}{{2 \cdot 50(1 + 1)}} = 20^\circ

En este caso sí se ha reducido significativamente el ángulo de visión cuando hemos pasado de una distancia de 55 cm a otra de tan sólo 10 cm.

Volver al menú principal del tutorial Fundamentos Ópticos en Fotografía