Curso Fundamentos Ópticos en Fotografía
Resumen
La profundidad de campo es mayor cuanto mayor sea el círculo de confusión permitido; es mayor cuanto más cerrado esté el diafragma (número f grande); es mayor cuanto mayor sea la distancia de enfoque. La profundidad de campo es mayor por detrás que por delante (casi siempre).
Vamos a obtener la ecuación que calcula la profundidad de campo. Puedes saltarte la derivación e ir directamente a las conclusiones si no te interesan las matemáticas.
Suponemos el modelo de lente delgada. Sabemos cómo obtener la imagen de un punto geométricamente mediante la teoría de rayos. Sabemos que todos los objetos situados a esa distancia aparecerán enfocados en el sensor. Sabemos que un punto situado delante de dicho plano formará su imagen antes del sensor, apareciendo como un círculo en la superficie del sensor. Para un punto por detrás, el efecto sobre el sensor es el mismo (en este caso la imagen se forma más allá del sensor).
Podemos resumir todo esto en el siguiente gráfico.
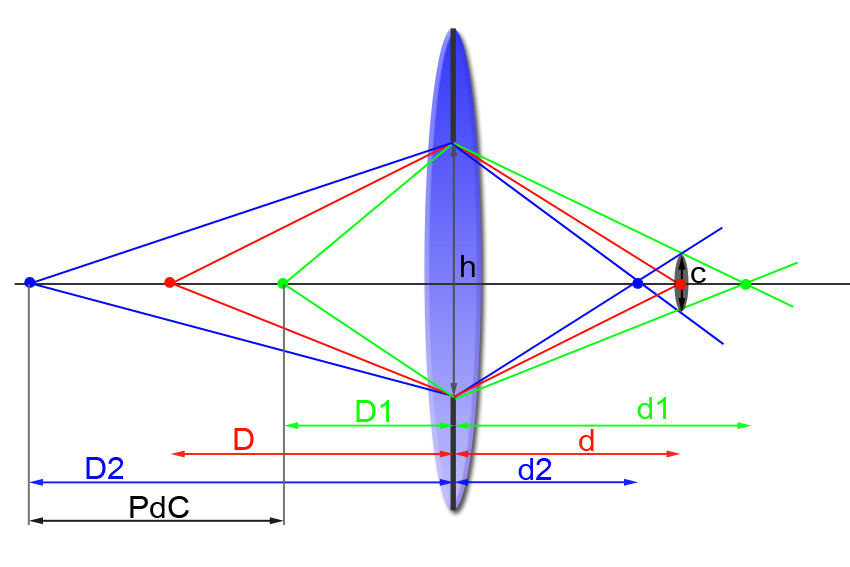
Figura 1. Ecuación de profundidad de campo
La abertura del diafragma es h. El punto rojo representa el plano enfocado. Está situado a una distancia D. La imagen se forma a una distancia d de la lente. Es ahí donde se encuentra el sensor. Los puntos por delante y por detrás no están enfocados, pero hasta que no produzcan un círculo de confusión de tamaño c aparecen como enfocados. El límite por delante lo marca el punto verde situado a D1. El límite por detrás lo marca el punto azul situado a D2. Cualquier objeto entre estas distancias aparecerá al ojo como enfocado, obteniéndose la profundidad de campo (PdC en adelante):
PdC = D2 - D1Así pues, el objetivo es obtener D2, D1 y con ello la PdC.
Estas distancias las obtenemos geométricamente utilizando triángulos semejantes y la ecuación de la lente. Si no te interesa puedes saltarte la demostración e ir directamente al resultado.
Del rayo verde en la zona imagen obtenemos la relación por triángulos semejantes (ver figura):
\frac{{d1 - d}}{{c/2}} = \frac{{d1}}{{h/2}}Del rayo azul,
\frac{{d - d2}}{{c/2}} = \frac{{d2}}{{h/2}}Podemos reorganizar estas ecuaciones en:
\frac{{d1 - d}}{{d1}} = \frac{c}{h} \frac{{d - d2}}{{d2}} = \frac{c}{h}Estas ecuaciones tienen un pequeño problema; que dependen de h, el tamaño real de la abertura del diafragma. Sin embargo, lo que se suele usar en fotografía es el número f, es decir, la abertura relativa del diafragma. Así que vamos a expresar esas ecuaciones en función del número f. Sabemos que el número f es la relación f/h, donde f es la distancia focal y h el diámetro de la abertura. Llamamos N al número f, con lo que tenemos: N = f/h. Sustituimos en las ecuaciones de antes el valor de la abertura absoluta h por la relativa N: h = f/N.
\frac{{d1 - d}}{{d1}} = \frac{{cN}}{f} \frac{{d - d2}}{{d2}} = \frac{{cN}}{f}El problema en estas ecuaciones es que están en función de las distancias en la zona imagen. Pero utilizando la ecuación de la lente podemos obtener sus equivalentes en la zona objeto.
La ecuación de lente delgada es:
\frac{1}{f} = \frac{1}{d} + \frac{1}{D}Y la podemos aplicar también para D1 y D2:
\frac{1}{f} = \frac{1}{{d1}} + \frac{1}{{D1}} \frac{1}{f} = \frac{1}{{d2}} + \frac{1}{{D2}}Así pues, tan sólo queda por sustituir d, d1 y d2 en función de D, D1 y D2 y la distancia focal f para obtener los valores:
D1 = \frac{{Df^2 }}{{f^2+cN\left( {D - f} \right)}} D2 = \frac{{Df^2 }}{{f^2-cN\left( {D - f} \right)}}Y por tanto, la PdC:
PdC = \frac{{Df^2 }}{{f^2-cN\left( {D - f} \right)}} - \frac{{Df^2 }}{{f^2+cN\left( {D - f} \right)}}Sí, tienes razón, nos ha salido una fórmula enorme; pero la vida a veces no es tan sencilla como a uno le gustaría.
Lo importante es que veas que la PdC depende del diafragma f, la distancia de enfoque D, la distancia focal f y el tamaño de círculo de confusión que consideres c. Y recuerda que esta ecuación es la de la lente delgada; en el caso de un objetivo real hay que tener en cuenta que las distancias se miden respecto al punto nodal delantero y trasero, que estudiaremos en el tutorial de Óptica Avanzada.
De la ecuación, podemos concluir que:
- La profundidad de campo es mayor cuanto mayor sea el círculo de confusión permitido.
- La profundidad de campo es mayor cuanto más cerrado esté el diafragma (número f grande, N en la ecuación).
- La profundidad de campo es mayor cuanto mayor sea la distancia de enfoque.
Lo que no resulta tan sencillo de ver es cómo depende la profundidad de campo de la distancia focal. Se suele decir que la profundidad de campo disminuye al aumentar la distancia focal (a igualdad de diafragma y círculo de confusión). Es decir, que un angular, 17 mm por ejemplo, tiene mayor profundidad de campo que un teleobjetivo, 200 mm por ejemplo.
Esto es cierto pero la comparación no es justa. Un angular tiene mayor ángulo de visión que un teleobjetivo, con lo que las dos fotos no son iguales. En la foto con el angular los objetos salen más pequeños (factor de magnificación menor), con lo que es normal que exista más profundidad de campo.
Sería más justo comparar las dos fotos con el mismo factor de magnificación, es decir, que los objetos tengan el mismo tamaño en las dos fotos.
Esto implica que tengamos que acercarnos en la foto hecha con el angular, con lo que cambia la distancia de enfoque y la comparación tampoco sería justa. En este segundo caso, las profundidades de campo son iguales.
Volver al menú principal del tutorial Fundamentos Ópticos en Fotografía
