Curso Fundamentos Ópticos en Fotografía
Resumen
La abertura relativa del diafragma se indica con el número f.
Cuanto más pequeño el número f, más luminoso es el objetivo (mayor abertura del diafragma).
El número f del diafragma
El número f mide la abertura RELATIVA del diafragma, ya que es el cociente de la distancia focal f y la abertura física real del diafragma D.
Número f o diafragma = f/D
Podemos expresar la luz que llega al sensor en función del número f.
En el artículo anterior acabamos de ver que dicho valor depende del cuadrado de la relación entre el tamaño de la abertura del diafragma y la distancia focal \left( {D/f} \right)^2 , así que sustituyendo la definición de número f, obtenemos que la iluminación de la imagen depende de la inversa del cuadrado del número f:
Luz proporcional a \left( D/f \right)^2 =(1/numero f)^2
Es decir, cuanto más pequeño el número f, más luz captura el sensor.
Además, esto significa que para una lente de distancia focal 100 mm y diafragma f/4, la abertura física del diafragma es D=100/4=25 mm.
Para un objetivo de distancia focal 50 mm y diafragma f/4, la abertura física se reduce a D=50/4=12.5 mm.
Sin embargo, a pesar de ser diferentes las dimensiones físicas del orificio del diafragma por donde entra la luz a la lente, ambas aberturas consiguen que incida la misma luz sobre el sensor, independientemente del objetivo que usemos, pues ambas tienen f/4.
Pero recuerda, esto sólo es cierto cuando suponemos que la distancia de enfoque es mucho mayor que la distancia focal, como suele ser el caso de la mayoría de fotos que haces.
Cuando la distancia de enfoque sea pequeña (del orden de la distancia focal) la imagen ya no se forma a la distancia focal, sino más lejos, con lo que habrá que calcular el número f equivalente, que ya no vendrá dado como la relación entre la abertura física del diafragma y la distancia focal.
Dicho de otro modo, un f/4 ya no garantiza la misma luz cuando enfocas un objeto muy cercano.
Ese tema lo trataremos en otro artículo, ya que es un asunto que afecta básicamente a la macrofotografía.
Quédate con la idea que como la imagen se forma más lejos la luz que llega al sensor es menor, así que un f/4 en macrofotografía es menos luminoso que un f/4 para una distancia de enfoque más lejana.
Escala de números f y dimensiones físicas de la abertura
Recuerda que número_f = f/D, así que D = f/número_f.
Es decir, que el diámetro físico real de la abertura del diafragma y el número f son inversamente proporcionales.
Para una misma distancia focal, si aumentas el doble el número f, el diámetro de la abertura se reduce a la mitad. Si divides por dos el número f, el diámetro de la abertura se hace el doble.
Por eso verás que objetivos de la misma distancia focal (por ejemplo un 70-200 de Canon), pasar simplemente de la versión f/4 a f/2.8 supone un cambio enorme en sus dimensiones físicas (y consiguiente rediseño y encarecimiento).
Manejar estas escalas puede ser un poco lioso al principio hasta que te acostumbras.
Para simplificar, cuando seleccionas números f muy altos, por ejemplo f/22, tu diafragma está muy cerrado; cuando seleccionas números pequeños, por ejemplo f/4, tu diafragma está muy abierto.
Escala de números f y exposición
Al fin y al cabo, a nadie le interesa las dimensiones físicas de la abertura del diafragma (salvo a los fabricantes).
Lo que nos importa es cómo afecta a la exposición el número f.
Como la luz depende del cuadrado de la inversa del número f, ocurre lo mismo que con el diámetro de la abertura multiplicado por dos.
Es decir, si pasas de f/4 a f/8 has aumentado por dos el número f, con lo que el diámetro se reduce a la mitad y la luz se reduce a una cuarta parte.
En Fotografía se habla de un punto o paso de exposición (f-stop en inglés) cada vez que multiplicas o divides por dos la luz: un punto más de luz es tener el doble de luz; un punto menos de luz es tener la mitad de luz.
Otra unidad muy usada es EV (Exposure Value). Se dice que la exposición aumenta +1EV cuando tienes un punto más de luz, y así sucesivamente.
Así que hablando en pasos, pasar de un f/4 a un f/8 es perder dos puntos de luz, -2EV, pues la luz se ha reducido a una cuarta parte.
Ahora no te resultará difícil entender la escala típica que se usa para dar el valor del número f: 1, 1.4, 2, 2.8, 4, 5.6, 8, 11, 16, 22, 32 (a veces también se indica como una relación: 1:1, 1:1.4, 1:2, 1:2.8, 1:4, …).
Para pasar del 2 al 2.8 hay que multiplicar por \sqrt 2 =1.41 . Pasar del 2 al 2.8 significa reducir el diámetro de la abertura en un factor \sqrt 2 y, lo que es más importante, reducir la luz en un factor \left( {\sqrt 2 } \right)^2=2 , es decir captar la mitad de luz.
Todo esto se puede resumir gráficamente con la siguiente figura:
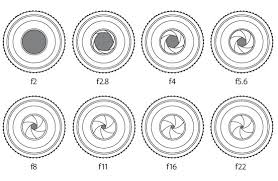
Si te mueves de izquierda a derecha, cada paso supone perder un punto de luz -1EV, por ej., de f/2 a f/2.8 o de f/11 a f/16.
Si te mueves de derecha a izquierda, cada paso supone ganar un punto de luz +1EV, por ej., de f/2.8 a f/2 o de f/16 a f/11.
Las cámaras actuales (según modelo) permiten hacer un ajuste de la exposición mucho más fino, en pasos de 1/3 de punto.
Por eso cuando pones la cámara en modo AV o A (prioridad al diafragma) cada vez que mueves la rosca tres pasos estás aumentando/disminuyendo la exposición en un punto.
Volver al menú principal del tutorial Fundamentos Ópticos en Fotografía

Muchas gracias por tus explicaciones claras y fundamentadas; se agradece que no huyas de las explicaciones matemáticas, como hacen otros autores, que parecen sentir un extraño pudor por utilizar números y fórmulas. Yo creo que una técnica no se conoce a fondo si no se sabe traducir a lenguaje matemático.
Hay algo que no comprendo en esto de la abertura del diafragma. Dices que para un mismo número f, la abertura física varía si varía la distancia focal. Entonces, si tengo un objetivo de longitud focal variable ¿significa eso que, manteniendo el mismo número f, el diafragma se abre y se cierra si varío la distancia focal? No me parece que ocurra eso con el objetivo que tengo ahora mismo en las manos. Aparentemente el diafragma no se mueve en absoluto al variar la distancia focal.
Saludos.
Hola. Sí, pero … (siempre hay un pero)
«Se agradece que no huyas de las explicaciones matemáticas»
Como decía Galileo «Las matemáticas son el lenguaje con el que Dios ha escrito el universo»
«Dices que para un mismo número f, la abertura física varía si varía la distancia focal»
Sí.Una forma muy intuitiva de verlo: los teleobjetivos suelen ser más aparatosos que los angulares (de largo para tener focales más largas, y de diámetro para que puedas obtener el mismo nºf. Otra forma de verlo es en un zoom típico 18-55 mm por ejemplo. Verás que suelen ser más luminosos para 18 mm que para 55 mm; por ejemplo para 18 mm puede ser un f/3.5 pero para 55 mm es un f/5.6 (es menos luminoso porque la apertura física es mayor y hacer un objetivo muy luminoso con una focal grande no es tan sencillo, si encima quieres que no tenga distorsiones, etc)
Pero, te estarás preguntando: sí, esto está muy bien, pero yo sigo viendo que para mi objetivo, «el diafragma no se mueve en absoluto al variar la distancia focal.»
Así que lo dicho es cierto, pero … (siempre hay un pero)
Un objetivo real se modela con una lente gruesa (el tutorial usa el modelo de lente delgada para simplificar la explicación, pero un objetivo de verdad está formado por muchos elementos, no sólo 1). De todas formas, los principios son los mismos; para entender el cambio, mira la ecuación de la lente delgada y fíjate que las distancias se miden respecto al centro; al tener varias lentes, un objetivo real se modela como UNA lente única pero ya no de anchura despreciable, con lo que aparecen dos planos principales (en la lente delgada sólo hay un plano, el que pasa por el centro óptico) y las distancias hacia cada lado se miden desde el plano principal correspondiente («distancia de enfoque»: desde plano principal primero hasta objeto y «distancia donde se forma la imagen»: distancia desde plano principal secundario hasta sensor). Como vea dos o tres personas como tú que les interesa el tema os amenazo con un tutorial sobre lente gruesa y su aplicación a objetivos reales.
Para más inri, hay muchas tecnologías para hacer objetivos (por ejemplo, para un gran angular, tienen que inventarse un diseño para que les quepa el espejo en las réflex; en el caso de un teleobjetivo usan la misma idea pero al revés, para que un tele de 300 mm no sea tan grande como debería ser si sólo tuviese una lente).
Resumiendo, para aplicar la fórmula del número f en un objetivo real, necesitas saber dónde está ese plano secundario. Busca para tu objetivo y puede que lo encuentres (no te asustes si ves que la distancia es mayor que el tamaño de tu objetivo o cosas más raras; depende del tipo de objetivo y cómo esté hecho el diseño). Y recuerda que el tamaño de diafragma que ves es el visto A TRAVÉS de las lentes (desmóntalo del cuerpo y mira el objetivo por delante y por detrás; si quieres ver el tamaño real del diafragma, deberías desmontar el objetivo quitando lente a lente hasta que te apareciera el diafragma, cosa que obviamente no creo que tengas ganas de hacer salvo que no te importe cargarte el objetivo).
Volviendo al principio, «Cuando las leyes de la matemática se refieren a la realidad, no son ciertas; cuando son ciertas, no se refieren a la realidad.» (atribuido a Einstein; no estoy seguro, porque nunca he encontrado la referencia exacta de la cita; seguramente con esto pase como con la Fotografía; la gente copia y pega y entonces algo se convierte en famoso/cierto porque mucha gente lo dice, independientemente de su valor de verdad)
Pues no todos comprendemos igual las matemáticas, que además de inciertas e inexactas, juegan mucho con los términos y definiciones que acaban confundiendo más que lo que explican. Por ejemplo yo soy muy visual y necesito visualizar la fórmula matemática en algún ejemplo para poderla entender. Veo que cada que trato de encontrar la explicación al por qué del número f, salen cosas nuevas que me van enredando más, mejor allí la dejo. Yo nomás quería saber de dónde venía el número f y cómo se obtenía matemáticamente. Aun así no recuerdo muchos términos de las fórmulas que tendré que investigar. Gracias.
No, esa apertura es intacta, lo que varía es el punto focal que se desplaza según las exigencias que hagas a tu zoom.
Yo me apunto al tutorial sobre la lente gruesa.
Un saludo.
Muy interesante la explicacion de los números F. Por mi parte lo agradezco, porque no todos consiguen explicarlo atraves de la matematicas. Puede que a muchos no lo interese de esta forma, pero pienso que es lindo estar por dentro de las cosas y no repetirlas sin saber bien de lo que se habla.