Curso Fundamentos Ópticos en Fotografía
Resumen
Qué es el diafragma y cómo regula la luz que llega al sensor
El diafragma
El diafragma es el dispositivo que permite regular los rayos de luz que entran por el objetivo y llegan al sensor. Es el equivalente al iris del ojo humano.
El diafragma está formado por un conjunto de varillas opacas que se abren y cierran a conveniencia a modo de abanico dejando una abertura de forma circular por donde pasan los rayos de luz.
La redondez de la abertura depende de la fabricación del diafragma y el número de hojas con que está hecho (de 5 en adelante).
Un modo de saber la forma geométrica que tiene el diafragma de un objetivo es viendo la forma que tiene el flare (ese reflejo de luz que te sale a veces en las fotos cuando apuntas hacia el Sol u otra fuente de luz muy potente).
Por ejemplo, el de la figura 2 tiene forma octogonal.
Otra forma de averiguarlo es pulsando el botón de previsualización de la profundidad de campo de la cámara mientras miras por el objetivo.
En un objetivo real, el diafragma se encuentra físicamente colocado en un punto intermedio del conjunto de lentes que forma el objetivo.
Regulación de la luz con el diafragma
Para explicar sus efectos de manera sencilla, seguiremos con el modelo simplificado de una única lente delgada.
El diafragma se coloca delante de la lente y según su abertura pasan más o menos rayos.
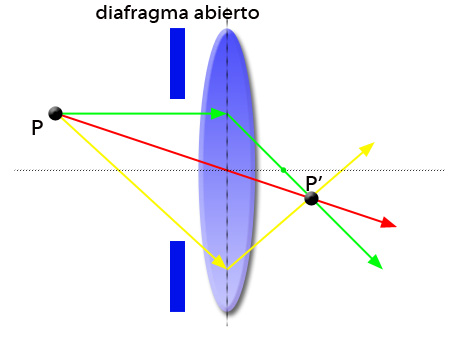
En la figura 3 hemos representado tres rayos provenientes del objeto P y cómo la lente los desvía para obtener la imagen P’.
Cuando el diafragma está muy abierto, los tres rayos consiguen atravesar la lente.
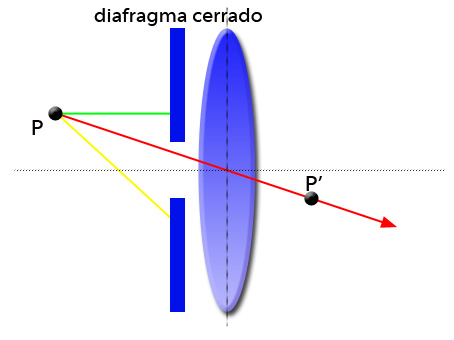
Sin embargo con el diafragma cerrado (figura 4) tan sólo el rayo rojo consigue atravesar la lente, con lo que la imagen pierde luminosidad.
Fíjate que el ángulo de visión es el mismo en ambos casos; es decir, el ángulo de visión no depende del diafragma.
Resumiendo, a medida que se va cerrando el diafragma, el haz de rayos que atraviesa la lente disminuye.
Dicho de otra forma, diafragmas cerrados captan menos luz que diafragmas abiertos.
El efecto visual es que la imagen se ve más oscura.
La figura 5 representa el haz de rayos que dejan pasar dos diafragmas diferentes.
Es evidente que el diafragma más grande (el verde) deja pasar más rayos de luz, con lo que la imagen que se obtiene es más luminosa.
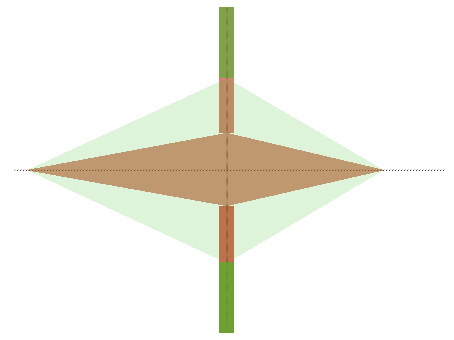
Figura 5. Regulación de la luz por el diafragma
Ya tenemos claro que un diafragma abierto capta más luz que otro cerrado, pero ¿cuánta más luz?
El diafragma: cuánta luz entra por el objetivo
Para eso necesitamos conocer cómo se relaciona la luz que entra en el objetivo con el tamaño de la abertura del diafragma.
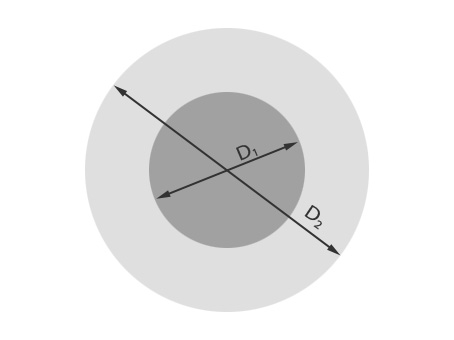
Puesto que el orificio por donde entra la luz es aproximadamente un círculo, la luz captada será proporcional al área S de dicho círculo:
S = \pi D^2 /4donde D es el diámetro del círculo.
Esto significa que si pasamos de un diafragma de diámetro D_1 a otro de diámetro D_2 , la relación de áreas es (ver figura 6):
\frac{{S_2 }}{{S_1 }} = \frac{{\pi D_2^2 /4}}{{\pi D_1^2 /4}} = \left( {\frac{{D_2 }}{{D_1 }}} \right)^2Es decir, el área aumenta proporcionalmente al cuadrado de la relación de los diámetros.
Dicha ecuación nos permite cuantificar cómo cambia la luz captada por un objetivo cuando cambiamos el diámetro de la abertura del diafragma.
Por ejemplo, si pasamos de un diámetro \(D_1\) a otro el doble \(D_2 =2D_1\), la luz captada se multiplica por cuatro (dos al cuadrado):
\left( {\frac{{D_2 }}{{D_1 }}} \right)^2 = \left( {\frac{{2D_1 }}{{D_1 }}} \right)^2= 2^2 =4Es decir, un diafragma de tamaño D_2= 2D_1 capta cuatro veces más luz que otro de tamaño D_1 .
Del mismo modo, si reducimos a la mitad el diámetro, la luz se reduce por cuatro.
Si queremos que la luz aumente el doble, debemos aumentar el diámetro en un factor \sqrt 2=1.41 , para que al elevarlo al cuadrado dé dos.
Ya sabemos cuánta más luz capta un diafragma respecto a otro. Pero la historia no acaba aquí.
El diafragma: cuánta luz llega al sensor (exposición)
Lo importante no es cuánta más luz capta un diafragma u otro en términos absolutos, sino cómo afecta eso a la luz que llega al sensor, es decir, la exposición de la foto.
Aquí aparece el segundo protagonista: la distancia de la lente al sensor (el plano donde se forma la imagen).
Cuanto más lejos menos luz llega; además esa relación también es cuadrática: es decir, que la intensidad de luz que llega al sensor es inversamente proporcional al cuadrado de la distancia 1/r^2 , donde r es la distancia del diafragma al sensor.
Si no lo ves claro, basta con que hagas la prueba con una linterna y verás como la intensidad de luz disminuye con el cuadrado de la distancia.
Juntando ambos factores, vemos que la luz que llega al sensor es proporcional al cuadrado del diámetro de la abertura del diafragma (más abierto, más luz) e inversamente proporcional al cuadrado de la distancia del diafragma al sensor (más lejos, menos luz).
Es decir, la luz que incide en el sensor es proporcional a \left( {D/r} \right)^2 , donde D es el diámetro de la abertura del diafragma y r la distancia de la lente al sensor (donde se forma la imagen enfocada).
Esto quiere decir que si aumentamos el diámetro de la apertura el mismo factor que la distancia del sensor a la lente, la exposición de la imagen es la misma.
Puesto que hemos dicho que la principal función del diafragma es regular la luz que capta el sensor (no la que entra por el diafragma), la unidad que debemos usar no es la abertura absoluta del diafragma, sino la abertura RELATIVA respecto a la distancia del sensor a la lente.
Es decir, el factor importante a la hora de definir la luminosidad de un objetivo es el cociente D/r, o sea, la relación entre el tamaño físico real del diafragma y la distancia del sensor a la lente.
Si la distancia de enfoque es lejana (al menos varias veces la distancia focal de la lente), ya vimos que la imagen se forma aproximadamente a la distancia focal.
En ese y sólo ese caso, podemos suponer que la distancia del sensor a la lente es igual a la distancia focal r=f. Sustituyendo en la expresión anterior D/r un valor de r=f, obtenemos que la luz que capta el sensor es proporcional a la relación entre el diámetro de la abertura y la distancia focal D/f.
A la inversa de la relación que acabamos de obtener, es decir, f/D, se le llama número f o simplemente diafragma y se suele expresar como, por ejemplo, f/4.
Ahora entiendes por qué se escribe con la /, pues se trata de un número adimensional que mide la abertura RELATIVA del diafragma, ya que es el cociente de dos distancias (que se suelen dar en mm): la distancia focal f y la abertura física real del diafragma D.
Número f o diafragma = f/D
Es el momento de estudiar el número f en profundidad y ver en qué influye.
Volver al menú principal del tutorial Fundamentos Ópticos en Fotografía



¡¡¡¡ Ufff !!!! Eso que dices de que «la intensidad de luz que llega al sensor es inversamente proporcional al cuadrado de la distancia» suena a conjuro mágico.
Es cierto lo que dices para fuentes puntuales de luz. Para fuentes puntuales, muy pequeñas respecto al observador, se cumple que la intensidad de la luz disminuye inversamente proporcional al cuadrado de la distancia de la fuente al observador. Pero en este caso que tratas aquí, el de un diafragma emitiendo luz hacia un sensor, no estoy seguro que se pueda asimilar al de una fuente puntual. Las aberturas reales de los diafragmas rondan algunos milímetros, al igual que el tamaño de los sensores. No se si se puede considerar el diafragma, sobre todo cuando está muy abierto, como una fuente de luz puntual respecto al sensor.
Yo creo, vamos, no creo, estoy convencido de que la explicación de que la luz disminuya de forma cuadrática según aumenta la distancia focal es otra, pero ahora me tengo que ir a hacer la cena (ayer fue el día de la mujer trabajadora) y no tengo tiempo de contar mi historia.
Un saludo
No estoy hablando de la ley inversa del cuadrado, sino que la relación entre la luminancia de un punto de la escena y la iluminancia que produce en el sensor depende de la inversa de la distancia de la lente al sensor (hablando con propiedad, de la distancia del punto principal trasero de la lente al sensor; esta distancia se aproxima a la focal para enfoques lejanos y ahí aparece el concepto de apertura relativa o número f). El ejemplo usado por mí es desafortunado pues induce a pensar en la ley inversa del cuadrado como ha ocurrido contigo.
Hola Jorge. Sigo sin verlo claro.
Yo me imagino una linterna encendida (la voy a considerar como una fuente puntual de luz) y me puedo creer que, porque me lo dicen los físicos y más o menos se puede medir, si me voy alejando de la linterna la intensidad de la luz decrece con el cuadrado de la distancia. Si a un metro la intensidad es X, a dos metros la intensidad habrá bajado a X/4.
Si ahora coloco un cristal transparente a un metro y medio yo creo que el efecto de éste en la intensidad de la luz es prácticamente nula y a la distancia de dos metros seguiré teniendo la misma intensidad que antes, X/4. El cristal, si es suficientemente caro, no interviene en la intensidad de la luz.
Ahora cambiemos la linterna por el Sol (que no deja de ser una linterna que está muy lejos y tiene mucha intensidad en su origen y por eso llega tan lejos). Si hago pasar su luz por un cristal ésta lo atravesará y al otro lado del cristal apenas notaremos que su intensidad baja por mucho que nos alejemos del cristal.
Si ahora cambiamos el cristal por una lente (también muy cara), lo único que yo creo que hace la lente es desviar los rayos, que seguirán su camino hasta que tropiecen con algo que los absorba, pero la lente no habrá menguado su intensidad.
Parece en el caso que tu explicas como si la lente recogiera la luz de la escena y después fuese la propia lente la que la volviese a emitir. Como si los puntos de la lente se convirtieran en nuevas fuentes de luz. Y yo eso no lo acabo de ver. Pienso en el cristal de antes y no creo que las moléculas o lo que sea del cristal se convierta en fuente de luz cuando está bajo la incidencia de la luz de una fuente.
La fuente de luz sigue siendo la fuente originaria de la luz, la linterna, el sol o nuestra escena. No veo cómo la lente (cristal) se convierte en ‘fuente de luz’.
Y hoy me tengo que ir a comer, un arroz caldoso me espera.
Según mis antiguos estudios, la ley del cuadrado solo es aplicable a fuentes puntuales.
Aquí estamos usando la «iluminancia» medida en lux, sobre una superficie plana emitida por una superficie «cuasi plana» formada por la optica.
La iluminancia cambia cuando modificas la distancia a la superficie de medida en esa relación cuadratica; ya que, siendo la superficie la misma, llega a ella una densidad esferica distinta de luz. A igualdad de lumenes emitidos, llegan menos lux
Pero en este caso no ocurre esto, ya que la distancia es fija; por lo que no se puede aplicar esa variación cuadrática.
PS. Lumen = candela por esteroradian. Lux= Lumen por metro cuadrado. Ver: https://es.wikipedia.org/wiki/Lux
Hola. No sé si has podido ver otro comentario previo sobre la misma temática. Para que quede claro para los que buscáis una explicación técnica más rigurosa, copio y pego un trozo de mi libro sobre Ruido y Sensores:

¿Quiere decir esto que?
Un objetivo de focal fija de 600mm de máxima apertura f4 por ejemplo y un 150-600 de apertura f5-6.3, cuando los dos tienen la misma apertura de diafragma es decir 6.3 dejan pasar la misma luz y por lo tanto llega en los dos la misma cantidad al sensor.
¿ dónde estaría la diferencia de precios?
Hola Jorge y participantes de este debate. A mí se me complicó algo que seguramente debe ser una estupidez de entender. Cuando en un lente me están indicando f/2.8, me están indicando una relación de valores o un valor absoluto??? Es decir, me están diciendo que la luminosidad de ese lente es la longitud focal dividida por 2.8 o el valor 2.8 es el resultado de esa división??? Lo que no me queda claro a partir de la expresión antes mencionada f/D es si una abertura 2.8 en un lente 17 mm es más luminosa que una abertura 2.8 en un 200 mm???? no estoy muy seguro que se entienda lo que pregunto!!! Ojalá que sí y sino, ni te preocupes!!! Muchísimas gracias. Saludos cordiales. Atte. JJD
El número f es una relación (por eso no tiene dimensiones; es la fórmula que dices y encontrarás en el tutorial). Se usa el número f precisamente para independizar lo luminoso que es un objetivo de la distancia focal. Un 17 mm con f/2.8 es igual de luminoso que un 200 mm con f/2.8. Lo que cambia es el tamaño físico de la apertura, pero eso a nadie le importa; lo importante es la luminosidad (bueno, al que tiene que cargar con 2 kilos más de teleobjetivo para poder tener un f/2.8 en vez de un f/4 sí le importa, sobre todo a su espalda). Puedes comprobar que el tamaño físico es más grande en un teleobjetivo que en un angular con mismo número f simplemente mirando de frente los dos objetivos, y verás que tienen tamaños diferentes, aunque los dos sean f/2.8, por ejemplo. Para entenderlo más fácil te pongo un símil: piensa en un cubo recogiendo agua de lluvia. Cuanto más grande el cubo más agua capta, pero si hay que repartirla en más superficie, al final toca la misma cantidad de agua por unidad de superficie. Un teleobjetivo tiene menor ángulo de visión (los objetos salen más grandes), luego necesitamos recoger más agua para que la cantidad de luz por unidad de superficie en el sensor sea la misma. Por eso el tamaño físico del cubo es más grande en un teleobjetivo; pero se compensa con que la imagen se forma más lejos (objetos salen más grandes), con lo que al final tenemos la misma cantidad de luz por unidad de superficie que es lo que cuenta, o sea, el número f.